Was this problem worth 300 points? Definitely yes. If you look at the standings, you will see that even many of the top contestants, including many advancers, struggled with it. That is because the problem tries to trick you into doing a lot of casework. On the other hand, there is a really short and simple solution:
Read below for an explanation why this works and how to implement it easily.
First of all, we have to check whether brute force works. There are Theta(n^2) different substrings. Reversing a single substring takes Theta(n) time, and comparing two outcomes takes O(n) time, so the brute force solution would run in Theta(n^3). For n=2500 that is too much, but not by a wide margin. Basically, anything better should already be fast enough.
Let's start by asking the fundamental question: How to make our string lexicographically smallest? Well, first of all, the first letter has to be as small as possible. Is the first letter the smallest one we have in our string? If yes, perfect: we keep it there and never touch it. In fact, let's just forget that it exists.
(Why can we do that? Isn't it sometimes optimal to reverse a substring that starts here anyway? Well, such a substring must end with the same letter it begins with. Additionally, it must be lexicographically smaller backwards than forwards. And whenever we have such a substring at positions 1..x, instead of reversing it we can always reverse the substring 2..x for a better result: after the reversal, the string will start with more copies of the smallest letter.)
Suppose that the first letter was indeed the smallest one available and that we decided to leave it in its place. What happens next? Well, clearly we can ask the same question again. Is the next letter of our string the smallest letter we have in the rest of our string? And again, there would be two possibilities. It either is the smallest one, or it is not.
Given the letters in our string, there is exactly one string such that the answer is always positive: the one where the letters are already sorted in ascending order. Clearly we cannot improve such a string, so we return {0,0}.
For any other string, we will sooner or later reach a position where the answer to our question will be negative for the first time. In other words, we just found the leftmost position with the following property: currently, we have a letter Y here, but somewhere to the right of it we have letters smaller than Y. Let X be the smallest of those letters.
Below we show one example how the situation may look like. (In the example, X ≥ 'c', Y > X, periods represent various characters that are greater than X.)
aaabbcccY......X....XX..X.....
In order to make our string as small as possible, we need to replace the current letter by a letter that is as small as possible. Clearly, the best we can get is X. And for each occurrence of X, there is exactly one valid move that brings this X to the current position: reversing the segment that starts with the current Y and ends with the X we want.
This gives us fewer than 2500 candidates for the optimal solution. We can simply check them all and pick the best one.
Here's the entire algorithm for the string "aabcyzcfechgc":
In the last step, we have three distinct 'c' we may choose. Choosing the first one produces the string "czyfechgc", choosing the second one produces "cefczyhgc", and choosing the third one produces "cghcefczy". Out of these three possibilities the second one has the lexicographically smallest result, so that is what we shall do.
When implementing this solution, we can make our life a bit simpler by actually forgetting about X. Once we found the character Y, we know that the optimal solution reverses some segment that starts with this Y. So we can try all of these intervals, without even looking at the letter on their other end. The optimal one is always among them.
Java code follows:
String reverse(String S, int i, int j) {
StringBuilder sb = new StringBuilder();
for (int k=0; k < i; ++k) sb.append( S.charAt(k) );
for (int k=j; k >= i; --k) sb.append( S.charAt(k) );
for (int k=j+1; k < S.length(); ++k) sb.append( S.charAt(k) );
return sb.toString();
}
public int[] solve(String S) {
int[] answer = {0, 0};
for (int i=0; i+1 < S.length(); ++i) {
char c = S.charAt(i);
boolean startHere = false;
for (int j=i+1; j < S.length(); ++j) if (S.charAt(j) < c) startHere = true;
if (startHere) {
String best = S;
for (int j=i+1; j < S.length(); ++j) {
String T = reverse(S,i,j);
if (T.compareTo(best) < 0) {
best = T;
answer[0]=i;
answer[1]=j;
}
}
break;
}
}
return answer;
}
The above code runs in O(n^2), where n is the length of the input string: For each letter we try as Y, we need O(n) time to check whether a smaller X exists. Then, for just one Y (the leftmost one with that property), we try O(n) possibilities, and evaluate each of them in O(n) time.
As an exercise, try coming up with a solution that runs in O(n log n), or even in O(n). (How to identify the best right end of the interval we are reversing? What property does it have?)
Again, let's start our solution with a basic sanity check. What would happen if we tried to solve this problem using the most obvious algorithm? The most obvious solution would probably look as follows:
With c cliques given in the input, the first part would take O(cn^2) time and the second part would run in O(n^3). We cannot get a better upper bound for the second part because the graph is dense: there are only n vertices, but there can easily be Theta(n^2) edges. Thus, for n=2500 the second part will be too slow, but not by a wide margin. Again, as in the easy problem in this round, it seems that any improvement will get us where we want to be.
The O(cn^2) seems equally intimidating, but in this case we are actually better off. This is because the problem statement implies not only a limit of c ≤ 2500 cliques, but also a limit of s ≤ 5000 on the sum of their sizes. And this actually makes our life easier. The worst possible input in terms of the number of edges are basically two cliques, each covering the entire graph, but this is still only Theta(n^2) edges. Thus, the first part would actually run within the time limit if we used brute force. (However, we will not be using brute force to generate all edges – we will be smarter, and that will help us to do the second part more efficiently.)
We will now show two different solutions. Well, they are basically the same solution, but their implementations will differ. The first solution is probably easier to discover but requires a bit more coding. The second solution uses a small technical trick, but then becomes really straightforward to implement.
Solution #1.
Imagine that we just started a BFS from a vertex in our graph. Also, imagine one particular clique C in our graph. How will the distances for the vertices on C look like? For some d, there will be vertices that have distance d from the source, and possibly some additional vertices that have distance d+1. Below this is explained in detail.
As the BFS runs, sooner or later it will reach the first vertex on C, and assign the distance d to this vertex. Then, the BFS keeps on processing vertices that have distance d-1 and discovering new vertices that have distance d. During this phase, it is possible that some additional vertices on C will be discovered and assigned the distance d.
Once this part is over, some (at least one) vertices on C have the distance d. These vertices are in the BFS queue, ready to be processed. All other vertices on C are still unvisited.
Finally, as soon as we get to process the first vertex, we will (among other things) use the edges of C to reach all other vertices on C, and each of them will be assigned the distance d+1. Note that this was the first and only time during the entire BFS when we used the edges in C to discover new information. In the future, when processing other vertices on C, the edges in C will not tell us anything new.
And that is precisely where the improvement comes. Here is the improved algorithm, in detail:
for each source vertex s:
mark all vertices and all cliques as unvisited
start BFS from s
when processing a vertex v during the BFS:
for each unvisited clique C that contains v:
mark C as visited
use edges in C to discover new vertices
Clearly, with n vertices and c cliques (with at most n vertices each), a single run of the BFS takes O(s) time, as we process each clique once, and the time needed to process a clique is linear in its size. Hence, the total time complexity is O(ns).
Solution #2.
If we want an easier implementation, we may preprocess the input as follows: Instead of adding a clique...

... we add a new vertex, and connect each of the original vertices to this vertex:
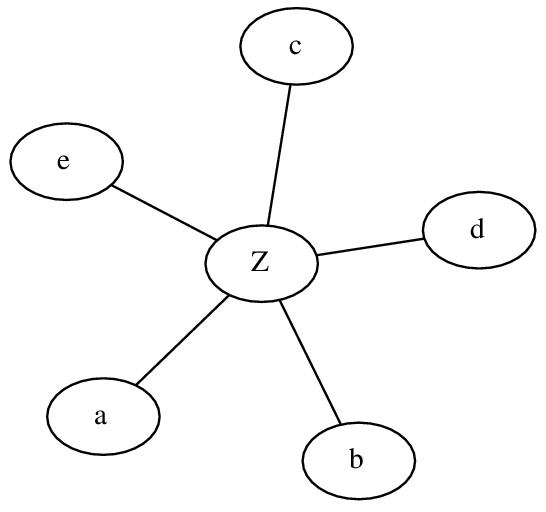
The effect is almost the same: Each pair of vertices that belong to the clique are now at distance 2 (instead of 1). The benefit should be clear: the number of edges we need is linear, not quadratic in the size of our clique.
Once we do this modification to our graph, we can use a standard BFS to compute the distances, and at the end we simply divide all distances by 2. The time complexity of this approach is also O(ns). C++ implementation follows.
long long calcSum(int N, vector <int> V, vector <int> sizes) {
vector<int> S(1,0);
for (int x:sizes) S.push_back( S.back()+x );
int Z = N + V.size();
vector< vector<int> > G(Z);
for (unsigned i=0; i<sizes.size(); ++i) {
// from each vertex in the clique, add a directed edge to the "clique vertex"
// and a directed edge from the "clique vertex" back
for (int j=S[i]; j<S[i+1]; ++j) {
G[ V[j] ].push_back( N+i );
G[ N+i ].push_back( V[j] );
}
}
long long answer = 0;
// for each vertex, run BFS to compute distances to other vertices
for (int n=0; n<N; ++n) {
vector<int> D(Z,123456789);
D[n] = 0;
queue<int> Q;
Q.push(n);
while (!Q.empty()) {
int src = Q.front(); Q.pop();
for (int dest : G[src]) {
if (D[dest] <= D[src]+1) continue;
D[dest] = D[src]+1;
Q.push(dest);
}
}
for (int i=n+1; i<N; ++i) answer += D[i]/2;
}
return answer;
}
When it comes to this problem, you all should thank the problem author that the examples actually illustrated many of the tricky test cases. With a weaker set of examples, I would expect close to zero correct solutions. And the reason would be the same as in the 300-pointer: the problem would draw you towards a solution that checks a lot of cases, and you would forget or mishandle at least one of them.
A solution using casework.
Of course, it is actually possible to solve the task this way. One possibility is to try building a valid permutation, with two possible outcomes: we either succeed, or we discover some contradiction along the way.
There are complications. For example, for n=10^9 we cannot even afford to actually build the valid permutation, nor can we afford to verify its existence one number at a time. Luckily, there are only few of those n numbers that are special: these are the numbers that actually appear in the input as the maxima of some segments.
We can imagine that we are placing the numbers into our permutation in batches. If the numbers mentioned in the input are b1 < b2 < ... < bK, we will have K+1 batches:
Suppose that we are currently placing a batch that ends with the number B. The input contains one or more intervals that are supposed to have B as their maximum. Immediately we get the first constraint on B: B has to lie in the intersection of all those intervals. If said intersection happens to be empty, there is no valid permutation. For example, it is not possible for the intervals [2,5] and [7,10] to both have the same maximum.
Let I be the intersection we mentioned in the previous paragraph: that is, I is the interval where we can place B. Can we choose any location in I and place B there? No, we cannot, because of the other intervals given in the input. Namely, any interval with a maximum strictly smaller than B cannot contain B. Hence, we get our second constraint: The union of all intervals with maxima smaller than B must not contain the entire interval I. Again, if all elements of I are forbidden by the intervals with smaller maxima, there is clearly no solution. For example, it is not possible for the interval [2,7] to have maximum 20 if the maximum in [1,6] is 8 and the maximum in [7,11] is 16.
Finally, once we place B onto any valid location, we have to fill in the rest of the intervals that are supposed to have maximum B. This gives us our third and final constraint: The total length of the union of all intervals with maxima smaller than or equal to B must not exceed B. For example, the interval [2,15] cannot have maximum 7 because there are more than 7 numbers in the interval.
Note that for the last batch (i.e., numbers greater than any number mentioned in the input) we don't have to verify any constraints.
All that remains is to check that if the above constraints are always satisfied, we can always construct a valid permutation. This should be fairly obvious: we place the numbers as outlined above, and whenever we have more than one choice, all valid choices are equivalent.
Suppose that there are x intervals given in the input. This gives us O(x) batches of numbers. For each batch of numbers, we do some operations while checking the constraints. The slowest of those operations is the computation of the union of some O(x) intervals. In the implementation below I do this using sweeping in O(x log x) time. Hence, the entire solution runs in O(x^2 log x). C++ implementation follows.
vector< pair<int,int> > get_union(const vector< pair<int,int> > intervals) {
vector< pair<int,int> > events;
for (auto tmp : intervals) {
events.push_back( { tmp.first, -1 } );
events.push_back( { tmp.second, +1 } );
}
sort( events.begin(), events.end() );
vector< pair<int,int> > answer;
int last_open = events[0].first;
int open_intervals = 1;
events.erase( events.begin() );
for (auto event : events) {
if (open_intervals == 0) last_open = event.first;
open_intervals -= event.second;
if (open_intervals == 0) answer.push_back( { last_open, event.first } );
}
return answer;
}
int sum_lengths(const vector< pair<int,int> > intervals) {
vector< pair<int,int> > all = get_union(intervals);
int answer = 0;
for (auto tmp : all) answer += tmp.second - tmp.first;
return answer;
}
string possible(int N, vector <int> L, vector <int> R, vector <int> ans) {
// for each value, the list of intervals where it is the maximum
map< int, vector< pair<int,int> > > events;
int Q = L.size();
for (int q=0; q<Q; ++q) events[ ans[q] ].push_back( {L[q],R[q]+1} ); // half-open interval
// get the list of values we have to process
vector<int> values;
for (auto tmp : events) values.push_back( tmp.first );
reverse( values.begin(), values.end() );
// for each value v: check whether we can place all values >= v
for (int v : values) {
// the intervals with maximum v must have a non-empty intersection
int lo=-1, hi=N+1;
for (auto tmp : events[v]) {
lo = max( lo, tmp.first );
hi = min( hi, tmp.second );
if (hi <= lo) return "Impossible";
}
// there must be enough room for all greater values
vector< pair<int,int> > forbidden;
for (int vv : values) if (vv <= v) for (auto tmp : events[vv]) forbidden.push_back(tmp);
forbidden = get_union( forbidden );
int forbidden_length = sum_lengths( forbidden );
if (forbidden_length > v) return "Impossible";
// no greater value must be forced to reside inside the impossible zone
for (int bv : values) if (bv > v) for (auto big : events[bv]) for (auto small : forbidden)
if (small.first <= big.first && big.second <= small.second)
return "Impossible";
}
return "Possible";
}
A solution using flows.
As the title of this section suggests, there was also an alternate way of solving this task: we can reduce it to maximum flow. We will show the construction on an example.
Consider the following test case: n=100, and the intervals and their maximums are the following ones: [10,30) -> 47, [20,42) -> 47, and [15,78) -> 95. Note that I'm using half-open intervals: the interval [10,30) does contain cell 10 but it does not contain cell 30.
The endpoints of the intervals given in the input divide the array into some parts: "basic intervals". In our case, these parts are [1,10), [10,15), [15,20), [20,30), [30,42), [42,78), and [78,101). We are going to take the numbers 1 through 100 and distribute them into these parts somehow.
We can also divide the numbers into parts – almost like in the previous solution. The only difference is that now it will be better to treat the numbers given in the input separately. Thus, in our example, we have five "types of numbers": [1,47), 47, [48,95), 95, and [96,101). In our code, we represent each type of numbers by its smallest representative (in our example: 1, 47, 48, 95, and 96).
For each type of numbers, we know their count, i.e., how many such numbers we need to distribute. For each basic interval, we know how many numbers fit inside. The only thing that remains: for each pair (type of numbers T, basic interval B) we have to determine whether we may place such numbers into that particular interval. Luckily for us, this is also easy. There are only two situations when you cannot place numbers into an interval:
Using the above constraints, we can build a simple flow network: a source, one vertex for each type of numbers, one vertex for each basic interval, and a sink. We then find the maximum flow in our network. If its size is n, we just constructed a (class of) valid permutation(s). Otherwise, we can be certain that no valid permutations exist.
C++ implementation follows (maximum flow computation has been omitted).
string possible( int n, vector <int> QA, vector <int> QB, vector <int> ans ) {
int Q = QA.size();
for (int q=0; q<Q; ++q) ++QB[q]; // making the intervals half-open
set<int> s_number_types;
s_number_types.insert(1);
s_number_types.insert(n+1);
for (int x:ans) s_number_types.insert(x);
for (int x:ans) s_number_types.insert(x+1);
vector<int> number_types( s_number_types.begin(), s_number_types.end() );
set<int> s_interval_boundaries;
s_interval_boundaries.insert(1);
s_interval_boundaries.insert(n+1);
for (int x:QA) s_interval_boundaries.insert(x);
for (int x:QB) s_interval_boundaries.insert(x);
vector<int> interval_boundaries( s_interval_boundaries.begin(), s_interval_boundaries.end() );
int T = number_types.size()-1, B = interval_boundaries.size()-1;
MaxFlow<int> MF;
// vertices in the max flow graph:
// 0 = source
// 1..T = number types
// T+1..T+B = basic intervals
// T+B+1 = sink
// add source -> number_type edges, capacity = count of numbers
for (int t=1; t<=T; ++t) MF.add_arc( 0, t, number_types[t]-number_types[t-1] );
// add basic_interval -> sink edges, capacity = length of interval
for (int b=1; b<=B; ++b) MF.add_arc( T+b, T+B+1, interval_boundaries[b]-interval_boundaries[b-1] );
// add number_type -> basic_interval edges, capacity = either 0 or n
for (int t=1; t<=T; ++t) for (int b=1; b<=B; ++b) {
bool add = true;
// condition 1: basic_interval b must not have a smaller maximum
for (int q=0; q<Q; ++q)
if (QA[q] <= interval_boundaries[b-1] && interval_boundaries[b] <= QB[q])
if (number_types[t-1] > ans[q])
add = false;
// condition 2: there must not be an interval with the given maximum elsewhere
for (int q=0; q<Q; ++q)
if (ans[q] == number_types[t-1])
if (QB[q] <= interval_boundaries[b-1] || interval_boundaries[b] <= QA[q])
add = false;
if (add) MF.add_arc( t, T+b, n );
}
int flow = MF.getFlow( 0, T+B+1 );
return flow==n ? "Possible" : "Impossible";
}